Introduction to Gates and Circuits
/ 6 min read
This work is supported by a grant from the Mina Foundation
Arithmetic Circuits: Gates and Constraints
At the core of zk-SNARKs, including the math powering Mina, is a powerful concept called arithmetization. The basic idea is that we can transform program into arithmetic circuits which can then be represented as low-degree polynomials. These circuits represent computations as a network of interconnected gates, where each gate performs simple arithmetic operations. The correctness of the computation is enforced through a system of constraints that the prover must satisfy to generate a valid proof.
Here you can see an extremely simple circuit in action.
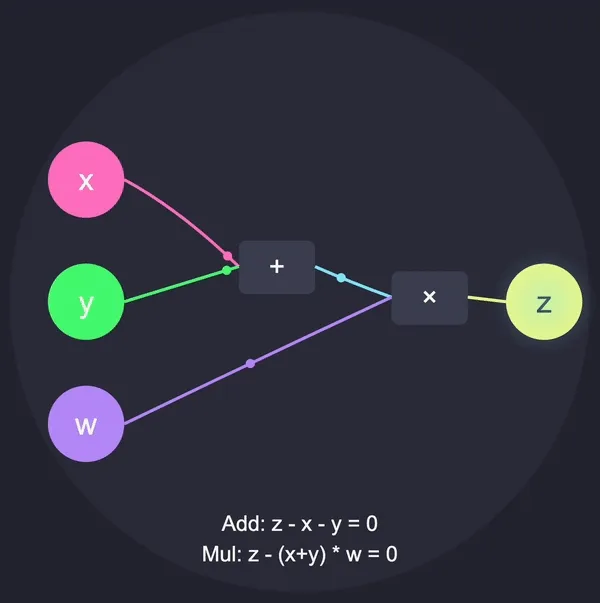
Explanation:
- Add Gate: Takes inputs ( x ) and ( y ) and outputs ( x + y ).
- Mul Gate: Takes the output of the Add gate (( x + y )) and input ( w ), computing ( (x + y) * w ).
Mina uses a popular form of arithmetization called Plonkish. In this note, we will do a high-level overview of basic gates and then do a deep dive into the Plonkish arithmetization used in Kimchi. This will set us up to think about the core cryptographic protocol at a much deeper level.
2. Introduction to Basic Gates
To enforce the correctness of computations within zk-SNARKs, each gate in the arithmetic circuit is associated with specific constraints. These constraints are algebraic equations that must hold true for the computation to be considered valid.
2.1. Addition Gate
Operation:
Constraint Equation:
Intuition: This equation ensures that the output is exactly the sum of inputs and .
2.2. Multiplication Gate
Operation: Constraint Equation: Intuition: This equation ensures that the output is exactly the product of inputs and .
2.3. General Gate Constraint
In a more generalized setting, a gate can enforce a linear combination of inputs and outputs. For example: Where are coefficients, and is a constant term.
3. Constraint Systems
A constraint system translates the computational logic of an arithmetic circuit into a set of algebraic equations that must be satisfied for the computation to be valid. In the context of arithmetization within zk-SNARKs, these constraints are often represented using matrices, enabling efficient mathematical manipulation and proof generation.
3.a. Arithmetization Using Matrices
Arithmetization involves converting logical computations into algebraic forms. Representing constraints as matrices facilitates leveraging linear algebra techniques for efficient computation and verification. Let’s explore how this abstraction is introduced and utilized.
3.a.1. Matrix Representation of Constraints
Consider an arithmetic circuit with multiple gates, each enforcing specific constraints. These constraints can be organized into matrices to systematically represent the relationships between variables and operations.
-
Variables Vector (): A vector containing all the variables in the circuit, including inputs, outputs, and intermediate values.
-
Constraint Matrix (): A matrix where each row represents a constraint equation, and each column corresponds to a variable.
Here, is an matrix (with constraints and variables), and is a vector representing the constants in each constraint equation.
3.a.2. Example: Matrix Formulation
Suppose we have a simple constraint system:
To represent this system using matrices:
-
Linearize the Constraints:
The first equation is linear, but the second is quadratic. To handle non-linear constraints, zk-SNARKs typically linearize them using auxiliary variables or polynomial representations. For simplicity, let’s assume all constraints can be linearized.
-
Define the Constraint Matrix () and Constants Vector ():
Here, each row of corresponds to a constraint equation, ensuring that .
3.a.3. Importance of Matrix Representation
- Scalability: Efficiently handles large numbers of constraints and variables.
- Linear Algebra Techniques: Facilitates the use of polynomial commitments and evaluations.
- Optimization: Enables optimizations in proof generation and verification by exploiting matrix sparsity and structure.
3.c. Transitioning from Gates to Constraint Systems
Understanding how individual gates translate into a global constraint system is crucial. Let’s explore this transition with a high-level diagram and step-by-step explanation.
3.c.1. Step-by-Step Transition
-
Define Gates:
- Gate 1: Logical AND to compute
- Gate 2: Multiplication to compute
- Gate 3: Logical OR to compute
-
Translate Each Gate to Constraints:
-
Gate 1 Constraint:
-
Gate 2 Constraint:
-
Gate 3 Constraint:
-
-
Assemble Constraints into a System:
Combine all constraints into a matrix form:
Where includes all variables involved.
-
Matrix Representation:
The constraint matrix systematically encodes the relationships imposed by each gate, ensuring that the entire computation adheres to the intended logic.
3.c.2. Visual Illustration: Gates to Constraints
To further clarify the transition, consider the following diagram illustrating how individual gate constraints contribute to the overall constraint system.
+---------+ +---------+ +---------+| Gate 1 | | Gate 2 | | Gate 3 || AND | | MUL | | OR |+---------+ +---------+ +---------+ | | | v v vConstraint 1 Constraint 2 Constraint 3 | | | +---------+--------+---------+--------+ | | Constraint System Matrix | [ A ] · [v] = 0Explanation:
- Gates: Represent the logical and arithmetic operations.
- Constraints: Algebraic equations derived from each gate’s operation.
- Constraint System Matrix (): Aggregates all constraints into a linear algebraic form, facilitating efficient proof construction and verification.
3.d. Mathematical Formulation and Intuition
To solidify understanding, let’s formalize the constraint system using matrix notation and explore the mathematical intuition behind it.
3.d.1. Polynomial Representation
In zk-SNARKs, constraints are often represented as polynomials evaluated over a finite field. Each gate’s constraints contribute to a global polynomial that must evaluate to zero across the entire domain.
-
Gate Constraints:
For each gate :
Where:
- and are selector polynomials determining the gate type.
- , , and are polynomials representing the left input, right input, and output of gate .
-
Global Constraint Polynomial:
3.d.2. Matrix Representation Revisited
The polynomial constraints can be represented in matrix form for computational efficiency:
Where:
- encodes the coefficients from all constraints.
- is the vector of variable assignments (including intermediate variables).
3.d.3. Intuition Behind Matrix-Based Constraint Systems
- Linearization of Constraints: By organizing constraints into a matrix, complex computations are transformed into linear algebra problems, which are well-understood and efficiently solvable.
- Scalability: Matrix operations scale gracefully with the size of the computation, allowing zk-SNARKs to handle large circuits.
- Polynomial Commitment: Leveraging matrices aligns with polynomial commitment schemes used in zk-SNARKs, facilitating secure and efficient proof generation.
3.e. Summary of Constraint Systems Formulation
- Matrix Abstraction: Constraints are systematically organized into matrices, enabling the use of linear algebra for efficient computation and verification.
- Mathematical Foundation: Polynomial and matrix representations provide a robust mathematical framework for understanding and implementing zk-SNARKs in the real world protocol.
By mastering the formulation of constraint systems through matrices and understanding the translation from gates to algebraic constraints, we lay the groundwork for deeper exploration into more advanced topics like PLONK-specific mechanisms and lookup tables within the Mina protocol.